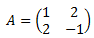Matrices

MATRIZ

Una matriz es un arreglo de números (llamados entradas de la matriz) ordenados en filas y columnas, donde una fila es cada una de las líneas horizontales de la matriz y una columna es cada una de las líneas verticales.

A una matriz con (n) filas y (m) columnas se le denomina matriz (n-por-m) escrito (n x m) donde (n, m) pertenecen a los números naturales exceptuando el cero. El tamaño de una matriz siempre se da con el número de filas primero y el número de columnas después.

Una matriz se representa por medio de una letra mayúscula(A,B…) y sus elementos con la misma letra en minúscula (a,b...), con un doble subíndice donde el primero indica la fila y el segundo la columna a la que pertenece.

EJEMPLO:

En el ejemplo vemos que la matriz esta nombrada con la letra (A) en mayúscula, y todas sus entradas tienen esta misma letra pero en minúscula (a).

En esta parte de la matriz, vemos como son nombradas las entradas de esta; en el caso de la entrada (a32) notamos que se nombra primero el numero de la fila que es (3) y luego el numero de la columna que es (2).

OPERACIONES DE MATRICES.

A). Suma: Se define la suma de dos matrices como la suma de (A+B) donde el requisito para poder realizar esta operación es que ambas matrices A y B  sean de igual tamaño, al realizar la suma de matrices  se realiza sumando la entrada de A con la misma entrada en B . (a12 + b12).

EJEMPLO:

En el ejemplo lo primero que vemos es que son matrices de igual tamaño y por lo tanto se puede efectuar la suma; también vemos como en la matriz resultante (A+B) se suman las entradas de la matriz A mas las entradas de la matriz B. y tenemos como resultado la matriz (A+B) Marcada de azul. 

Propiedades de la Suma:

        

              - Asociativa:

                                         (A + B) + C = A + (B + C)

              

             - Conmutativa:

                                         (A + B) = (B + A) 

                    

B). Producto de un Escalar por una Matriz: Se define producto de un escalar por una matriz, a una matriz A=(n x m) que es multiplicada por un numero real (K), donde cada elemento de la matriz (A) es multiplicado por (K).

EJEMPLO:

En el ejemplo vemos como cada una de las entradas de la matriz formada de 3x3 es multiplicada por el numero 2, dando como resultado la matriz que esta marcada en color azul.

C). Producto de Matrices: Se define la multiplicación de matrices como el producto de (A * B) donde el requisito para efectuar la operación, es que el numero de columnas de (A) sea igual al numero de filas de (B). Para realizar el producto se hace multiplicando la entradas de filas en (A) por entradas de columnas en (B). de la siguiente manera (a11 * b11) + (a12 * b21) + (a13 * b31) y asi sucesivamente hasta resolver todo el producto.

EJEMPLO:

En el ejemplo vemos primeramente que el numero de columnas de la primera matriz (A) es igual al numero de filas de la segunda matriz (B), por lo tanto se puede realizar el producto, luego vemos como las entradas de las filas de (A) multiplican las entradas de las columnas de (B), dando como resultado la matriz marcada de azul.

Propiedades del Producto:

             - Asociativa:

                                         (A * B) * C = A * (B * C)

              

             - Conmutativa:

                                         (A * B) =/= (B * A) -No es Conmutativa.

             - Distributiva respecto a la suma:
                                         A * (B + C) = A * C + A * B

MATRIZ TRANSPUESTA.

Dada una matriz A, se llama matriz transpuesta al cambio de orden de entradas de esta matriz, donde las filas de (A) pasan a ser columnas en (A).

EJEMPLO:

En el ejemplo vemos claramente que la matriz (A) al ser transpuesta cambian de orden sus filas y columnas, y lo que eran las filas en (A) pasan a ser columnas en A transpuesta como se indica en l matriz marcada de color azul.

MATRIZ BINARIA.

Una matriz binaria de (m x n), es una matriz en donde todas sus entradas son bits. Esto significa, que cada una de sus entradas tiene un valor de 1 o 0.

EJEMPLO:

En el ejemplo la matriz (A), es una matriz binaria de (6 x 6).

OPERACIONES DE MATRICES BINARIAS. 

Las operaciones de matrices se pueden calcular de manera muy fácil por el hecho de que sus entradas son 1 y 0, las operaciones las podemos calcular por medio de las siguientes tablas:

MATRIZ INVERSA POR COFACTORES

La matriz adjunta, o de cofactores de la matriz A que denotamos por Adj(A), es la matriz cuyo elemento (i, j)(fila i ; columna j) es el adjunto ad _{i , j} = ( - 1 ) ^{i + j} · det( A ^{i , j} ) donde la matriz A ^{i , j} es la matriz que resulta al quitar a la matriz A la fila i y la columna j.

Se cumple que la matriz inversa de A, A ^-1 se puede escribir en función de su adjunta como:

donde la notación de la potencia T expresa transposición de matrices.

Notemos que en la expresión anterior se divide por el determinante, con lo que éste no puede ser cero. Esto es obvio ya que si esto ocurre, la matriz es singular (no regular) y, por tanto, no tiene matriz inversa.

EJEMPLO:

Calculamos los cofactores de A (los elementos de su matriz adjunta).

La matriz adjunta es:

Calculamos el determinante de A:

La matriz inversa es:

Explicación:

Sistemas de Ecuaciones Lineales

SISTEMAS DE ECUACIONES LINEALES

     

      En álgebra lineal, un sistema de ecuaciones lineales, también conocido como sistema lineal de ecuaciones, es un conjunto de cuitas en paracaídas ecuaciones lineales (es decir, un sistema de ecuaciones en donde cada ecuación es de primer grado), definidas sobre un cuerpo o un anillo conmutativo.

SISTEMA DE ECUACIONES LINEALES (2X2).

Un sistema de ecuaciones lineales de 2x2 es aquel que contiene 2 ecuaciones de primer grado con 2 incógnitas, se llama solución de un sistema 2x2 a cualquier pareja de valores de X e Y que sean solución de ambas ecuaciones a la vez; los sistemas de ecuaciones 2x2 se pueden resolver por medio de los siguientes métodos:

A). Método de Reducción: Consiste en hacer que se anule una de las incógnitas en las dos ecuaciones. Esto se puede conseguir mediante:

    - La multiplicación de ambas ecuaciones por un número entero.

    - La multiplicación de una de las ecuaciones por un número entero.

    - La suma de las dos ecuaciones sin modificarlas previamente. 

Cuando tenemos las ecuaciones preparadas para que se anule alguna incógnita, las sumamos y despejamos la incógnita que nos queda. Después sustituimos en una de las ecuaciones la incógnita que acabamos de averiguar por su valor y, finalmente, despejamos la incógnita que nos falta por averiguar.

EJEMPLO:

B). Método de Igualación: El método de igualación consiste en despejar la misma incógnita en las dos ecuaciones que componen el sistema e igualar las dos expresiones, formando una ecuación que habremos de resolver. Cuando hemos obtenido el valor de la incógnita, cogemos ese valor y lo ponemos en una ecuación para así, obtener la incógnita que nos falta.

EJEMPLO:

C). Método de Sustitución: El método de sustitución consiste en despejar una incógnita en cualquiera de las dos ecuaciones, preferiblemente la que tenga menor coeficiente y a continuación sustituirla en otra ecuación por su valor.

EJEMPLO:

SISTEMA DE ECUACIONES LINEALES (3X3).

Un sistema de ecuaciones lineales de 3x3 es aquel que contiene 3 ecuaciones de primer grado con 3 incógnitas, se llama solución de un sistema 3x3 a cualquier conjunto de valores de X, Y, Z,  que sean solución de las 3 ecuaciones a la vez; los sistemas de ecuaciones 3x3 se pueden resolver por medio de los métodos vistos anteriormente y por el siguiente:

A). Regla de Cramer: